有讀者或許對於靜水壓為何突然增大不明白，有待筆者進一步做出相關之說明和解釋。基本上，靜水壓會增大可概分為以下兩種原因：
一、在海嘯或洪水發生時，靜水壓由於水頭高程不同，以致於產生水壓差突然增大；
二、地震或劇烈撞擊土壤，以致於靜水壓突然增大。
其中，讀者比較不清楚之處，應該是第二點所提地震引致之靜水壓增大問題。筆者以地震觀測站之加速度計（強震儀），其地震引致之地表加速度對於土壤之動力行為，作一簡單之土壤動力分析（國際單位制），即可了解筆者所欲表達之意思。土壤經地震擾動，其運動方程式為
+c\dot{u}\left ( t \right )+ku\left ( t \right )=-m\ddot{u_{g}}\left ( t \right ) "m\ddot{u}\left ( t \right )+c\dot{u}\left ( t \right )+ku\left ( t \right )=-m\ddot{u_{g}}\left ( t \right )")
在等號右側之項次-müg(t)，為該運動方程式之地震力，而左側之項次mü(t)，為土壤受地震擾動引致之慣性力。土壤之組成，包括土壤顆粒和孔隙水，在一般擾動情形下，土壤顆粒之接觸關係並不發生變化，而是孔隙水由於地震引致之慣性力，致使其流竄於土壤顆粒間之孔隙，以產生所謂之「超額孔隙水壓」。土壤孔隙水壓之計算，除考慮既有之靜水壓外，尚需考慮地震引致之慣性力，亦即土壤孔隙水壓為
}{A_{w}} "u=\gamma h+\frac{m_{w}\ddot{u_{g}}\left ( t \right )}{A_{w}}")
在土壤動力分析取üg(t)之最大值üg，並將mw/Aw以ρ表示水之面密度，則式子得簡化為
符號列表
舉例來說，地下水位於地表深度2米處，在設計水平地表加速度400gal下，試計算其孔隙水壓在地表深度2~8米處之變化。
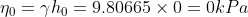
=58.8399kPa "\eta_{1}=\gamma h_{1}=9.80665\times \left ( 8-2 \right )=58.8399kPa")
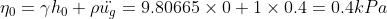
+1\times 0.4=59.2399kPa "\eta_{1}=\gamma h_{1}+\rho \ddot{u_{g}}=9.80665\times \left ( 8-2 \right )+1\times 4=62.8399kPa")
從上列計算可知，孔隙水壓整體增加0.4kPa，該值乃是由地震力所引致之慣性力，亦即所謂之超額孔隙水壓。超額孔隙水壓為尋求釋放其水壓力，必然四處流竄並進而破壞土壤接觸關係，以致於土壤液化行為之產生。靜水壓在地震作用下，將是引發土壤液化的關鍵原因。然而，深層土壤較為緊密，亦即靜水壓越來越高，而土壤也越來越緊密。
以上，即是有關於靜水壓和超額孔隙水壓之相關解釋和說明。在進階土壤動力分析方面，若是涉及需要推導運動方程，筆者推薦採用Lagrange運動方程，因為該方法可謂最為通用之簡單推導方法。D'Alembert是靜力分析法，但是由於其屬於矢量方法之一種，所以在有分布質量和彈性恢復力之結構上，將無法進行運動方程式之推導，因而在工程應用上相當少見該方法之使用。Lagrange僅需寫出動能（T）、位能（V）及非有勢力（Q），然後將式子原封不動地輸入Mathematica，即可獲得完全正確之運動方程式。因此，該方法既簡單又不會錯誤，是廣為工程使用之運動方程推導方法。
-\frac{\partial T}{\partial \dot{q_{j}}}+\frac{\partial V}{\partial q_{j}}=Q_{j} "\frac{d}{dt}\left ( \frac{\partial }{\partial \dot{q_{j}}} \right )-\frac{\partial T}{\partial \dot{q_{j}}}+\frac{\partial V}{\partial q_{j}}=Q_{j}")
筆者學淺，以上僅扼要解釋和說明，期能獲得讀者之參考。
一、在海嘯或洪水發生時，靜水壓由於水頭高程不同，以致於產生水壓差突然增大；
二、地震或劇烈撞擊土壤，以致於靜水壓突然增大。
其中，讀者比較不清楚之處，應該是第二點所提地震引致之靜水壓增大問題。筆者以地震觀測站之加速度計（強震儀），其地震引致之地表加速度對於土壤之動力行為，作一簡單之土壤動力分析（國際單位制），即可了解筆者所欲表達之意思。土壤經地震擾動，其運動方程式為
在等號右側之項次-müg(t)，為該運動方程式之地震力，而左側之項次mü(t)，為土壤受地震擾動引致之慣性力。土壤之組成，包括土壤顆粒和孔隙水，在一般擾動情形下，土壤顆粒之接觸關係並不發生變化，而是孔隙水由於地震引致之慣性力，致使其流竄於土壤顆粒間之孔隙，以產生所謂之「超額孔隙水壓」。土壤孔隙水壓之計算，除考慮既有之靜水壓外，尚需考慮地震引致之慣性力，亦即土壤孔隙水壓為
在土壤動力分析取üg(t)之最大值üg，並將mw/Aw以ρ表示水之面密度，則式子得簡化為
| 土壤質量 | 土壤阻尼 | 土壤勁度 | |||
| 歷時水平土壤加速度 | 最大水平地表加速度 | 土壤孔隙水壓 | |||
| 水單位重 | 地下水位深度 | 孔隙水質量 | |||
| 孔隙水承壓面積 | 水之面密度 |
舉例來說，地下水位於地表深度2米處，在設計水平地表加速度400gal下，試計算其孔隙水壓在地表深度2~8米處之變化。
從上列計算可知，孔隙水壓整體增加0.4kPa，該值乃是由地震力所引致之慣性力，亦即所謂之超額孔隙水壓。超額孔隙水壓為尋求釋放其水壓力，必然四處流竄並進而破壞土壤接觸關係，以致於土壤液化行為之產生。靜水壓在地震作用下，將是引發土壤液化的關鍵原因。然而，深層土壤較為緊密，亦即靜水壓越來越高，而土壤也越來越緊密。
以上，即是有關於靜水壓和超額孔隙水壓之相關解釋和說明。在進階土壤動力分析方面，若是涉及需要推導運動方程，筆者推薦採用Lagrange運動方程，因為該方法可謂最為通用之簡單推導方法。D'Alembert是靜力分析法，但是由於其屬於矢量方法之一種，所以在有分布質量和彈性恢復力之結構上，將無法進行運動方程式之推導，因而在工程應用上相當少見該方法之使用。Lagrange僅需寫出動能（T）、位能（V）及非有勢力（Q），然後將式子原封不動地輸入Mathematica，即可獲得完全正確之運動方程式。因此，該方法既簡單又不會錯誤，是廣為工程使用之運動方程推導方法。
筆者學淺，以上僅扼要解釋和說明，期能獲得讀者之參考。
